机器学习(二) 人工神经网络(1)

补充

对上一章缺少的内容做一个补充:「没有免费午餐定理(No Free Lunch Theorem)」

❝

任何一个预测函数，如果在一些训练样本上表现好，那么必然在另一个训练样本上表现不好，如果不对数据在特征空间的先验分布有一定假设，那么表现好与表现不好的情况一样多

❞

因此没有任何一种情况下都最好的机器学习算法，这个定理告诉我们，如果不对特征空间的先验分布有假设，那么所有算法的表现都一样，同时不能片面夸大这个定理的作用，从而对开发新的算法丧失信心，需要时刻牢记这个定理的提醒：机器学习的本质是通过有限的数据在复杂的高维特种空间中预测未知的样本的属性与类别

人工神经网络的介绍

从人工智能这一学科诞生以来，就有两种学派此消彼长，第一种学派人为：人工智能模拟的是人类大脑对世界的认识，因此研究大脑的认知机理、总结大脑处理信息的方式 是实现人工智能的先决条件，我们把这一派称之为人工智能得到仿生学派，仿生学派认为，计算机算法只有深入的模拟大脑的认知机制以及信息处理方式，才能最终实现人工智能。而另一个学派认为，以现在以及可预见的未来，我们无法完全了解人脑的认知机理，另一方面，计算机与人脑具有截然不同的物理属性和体系结构，因此片面强调人脑对计算机的模仿，既不可能也不必须，人工智能的研究应该立足于现有计算机的物理属性和体系结构，用数学和逻辑推理的方法，从现有计算机体系中获得确定的知识，而不是一昧的强调对人脑的模仿。这一学派，我们称之为数理学派

其中人工神经网络就是仿生学派的代表，在1943年，心理学家「W.S.mcCulloch」和数理逻辑学家「W.Pitts」基于神经元的生理特征，建立单个神经元的数学模型，我们称之为MP模型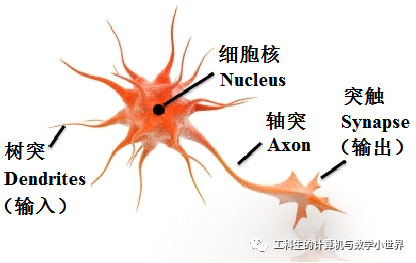

❝

这幅图是单个神经细胞的示意图，外部的刺激通过树突传递的神经元细胞核，经过细胞核加工后作为输出传递给突触。

❞

而「MP模型」是将外部刺激模拟成数字，将树突对刺激的加工过程模拟成权重对输入的加权，将神经元对输入的加工模拟成带有偏置的求和过程，最后的输出是对求和的过程进行非线性变换而输出。因此「MP」模型中，输入与输出的对应关系为

❝

❞

如果用向量的形式来表示，设，则可以记为

神经元的模型提出后，并没有引起学术界的重视，原因是该数学模型太简单，与实际相差甚远，无论是动物还是人，其神经元运行机制比这个复杂的多。从生物学的角度上来讲，人类至今没有搞清神经元的运行机制。下面从数学的角度为什么用这种加权求和的函数表达式来代替神经元的运作机制 ，设：神经元的输出是输入的函数：

❝

❞

对其进行泰勒展开

❝

❞

❝

❞

发现「MP模型」事实上是对一个复杂的函数进行一阶泰勒展开，值得一提的是，虽然神经元得到「mp」模型并不能反映真实的神经元运作机制，但是在机器学习领域中却非常有用，目前最常用的神经网络和深度学习的基本结构单元仍然是「mp模型」